Mathematical & computational analysis of the dynamics of structured neural network models
Recent advances in machine learning now allow us to construct complex artificial neural network models that have the potential to be more realistic and more capable than ever. However, it is typically very hard to dissect how the design choices made when building such models impact their performance or neural activity.
To overcome these difficulties, we develop theoretical approaches that strike a balance between maintaining key features of how the neural networks of interest perform their function while simplifying these models enough to permit mathematical tractability.
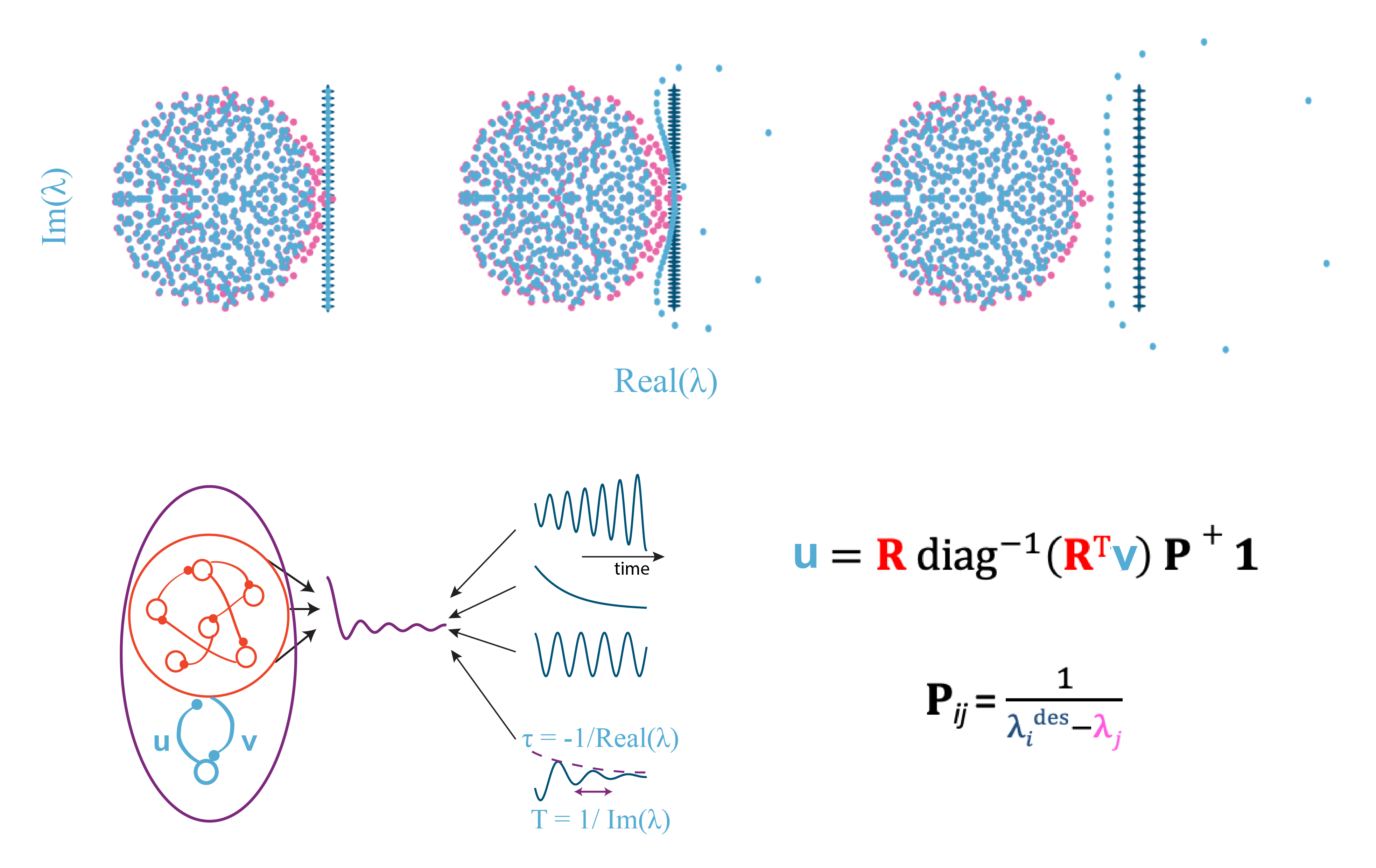
For instance, we have mathematically analyzed the dynamics of a recurrent (cortical) network modulated by a few loops. We constrained the neural response function to stay either in a linear or rectified regime, which both facilitates the mathematical analysis and is consistent with the dynamics that fit motor cortical activity well. However, even though it complicates the mathematical analysis, we preserved the expressivity of the network by accounting for task-optimized connections and allowing high-dimensional dynamics. Our ongoing work demonstrates that this framework can inform the design of robust, fully non-linear networks compatible with modern machine learning applications (see a related presentation, preprint, and use of a similar approach in Large Language Models).

In another line of research, we ask how to relate biological neurons to the simplified, smoothly varying artificial “units” used in the vast majority of modern neural network models on both the machine learning and theoretical fronts. Indeed, most mammalian biological neurons do not respond continuously to their inputs: instead, they emit a series of stereotypical signals called “spikes”. A line of work has related the average spike rate in a population of biological neurons to the continuous activity of model units. However, there remain challenges to account for the heterogeneity of connections among neurons of a population, as well as for dynamic properties of biological neurons - such as adaptation. We are making progress on these questions by deriving interpretable population rate equations that reflect key features of biological neurons while revealing the emergence of continuous state variables akin to those of artificial units.